hasemintelligence.blogg.se - Airfoil diagram

#AIRFOIL DIAGRAM FREE#

That the local pressure at the trailing edge is equal to free stream pressure is a coincidence - at lower angles of attack, the flow will decelerate below the free stream value near the trailing edge, so the blue region would wrap around the trailing edge. The stagnation point is below the highest distance between airfoil and pressure contour near the nose (in the blue region). P2 has no specific name here the flow accelerates through the free stream speed.

I recommend to use a different way of plotting pressure, see here for more.

Yes, measuring the perpendicular distance between the airfoil surface and the contour line will give you a pressure difference to the ambient pressure, but there is no scale, so all you can do is read relative pressures from that drawing.

Static pressure is equivalent to potential energy and total energy is constant, so this means that flow speed is higher than the free flow speed over the red region and lower over the blue region.

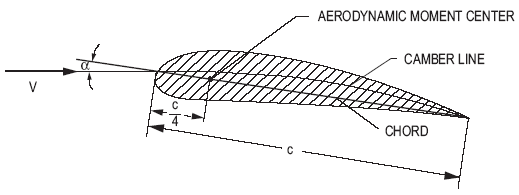
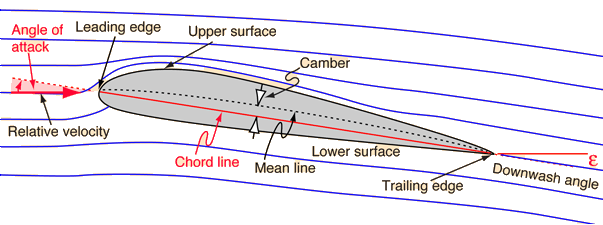
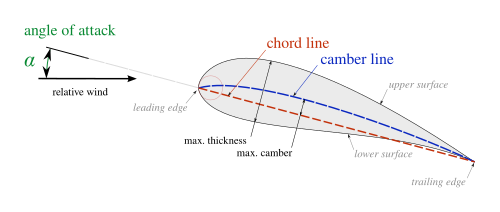
Yes, since the diagram shows the pressure distribution at high angle of attack, the top surface shows mostly suction (= local pressure is smaller than ambient pressure) and all of the bottom surface pressure that is higher than ambient pressure.While the camber-related part is constant, the angle-of-attack related part varies linearly with this parameter. In potential flow theory, the local pressure can be calculated as the linear superposition of a contribution from camber and one from angle of attack. Yes, this will change with angle of attack. The drawing in your answer shows the contour of the tips of the local pressure vectors when they are plotted perpendicularly to the local airfoil contour.What other elements can be deduced from the graphic? On the figure above, is p2 absolute pressure indeed equal to free stream air?ĭo point p2 and the similar one found on the trailing edge have specific names? What is the correct method to obtain the relative pressure at a given point p1? Is it to measure the length of the segment which is perpendicular to the airfoil surface at point p1? What is the scale? Is it correct to deduce from this diagram that the points on the red portion undergo a pressure smaller than free airstream static pressure, and those on the blue portion undergo a pressure greater than free airstream static pressure? In particular, diagrams like this are frequently seen when talking about airfoils:įrom Bernoulli or Newton's Laws for Lift?īeing not an aerodynamics engineer, I'll like to understand what can be deduced from this diagram.ĭoes this diagram indeed shows the variation of pressure on the contour of the airfoil ? Will this vary if the angle of attack or the speed are changed? My question is not about how this difference is generated, but only about the representation of the pressure around the airfoil. According to most authors, "lift is the result of the difference of pressure on airfoil sides".